e-PAL Algorithm for Multi-objective Optimization
What is it?
e-PAL (epsilon-Pareto Active Learning) is an algorithm designed to quickly predict the Pareto-optimal solutions in a multi-objective design space. This is particularly useful when measuring the target objectives is expensive, and therefore only a few samples of the design space should be drawn for measurement.
e-PAL predicts a Pareto front of the design space with the level of accuracy or granularity desired by the user. This granularity is specified with a vector parameter epsilon.
Assume that two objective functions are to be maximized simultaneously. The figure below shows an example of the true Pareto front of a design space contrasted with an epsilon-accurate Pareto front that could be predicted by e-PAL, with epsilon=(3,3).
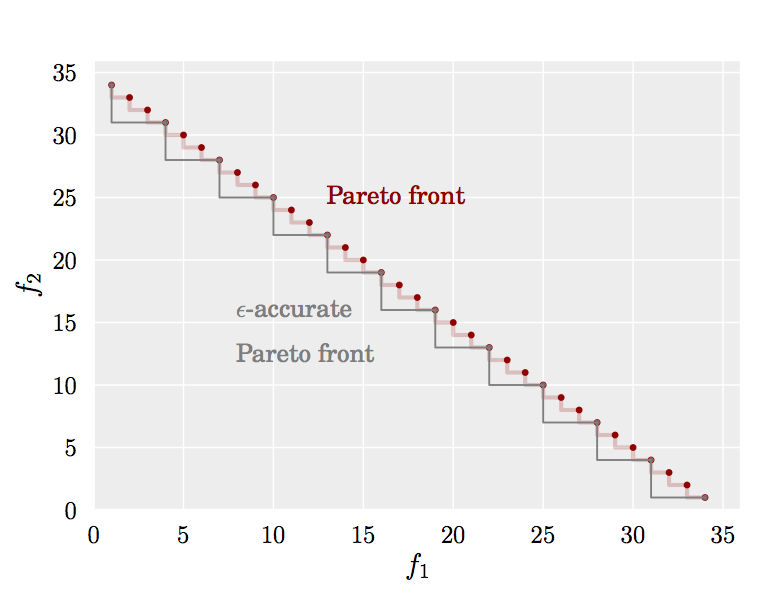
As shown in the figure, certain amount of redundancy can be removed when epsilon is greater than zero.
All our work on learning for optimization and autotuning.
Overview
The challenge of multi-objective design spaces is that rather than having a single optimal solution, several solutions may simultaneously optimize the target objective functions.
A concrete example in the domain of hardware design, are the design spaces generated by the Spiral DFT and sorting network hardware generators, when exploring the different settings provided by the tool. The user needs to choose between different candidate designs that perform the same task but that trade differently throughput and area. This challenge is aggravated by the fact that evaluating each design is extremely expensive, since complex synthesis processes must be executed. Thus, it is impractical and sometimes infeasible to evaluate every possible design in order to find the Pareto-optimal solutions that maximize throughput and minimize area at the same time.
e-PAL has several key features. Having drawn a few samples of the design space, it builds models using Gaussian processes to predict the objective functions for the rest of the space. Further, it uses the predictive uncertainty associated with these nonparametric models in order to guide the iterative sampling. Specifically, e-PAL's sampling strategy aims to maximize progress on designs that are likely to be Pareto-optimal. e-PAL iteratively discards points that are either redundant or suboptimal, and it terminates when no more points can be removed in order to guarantee that, with high probability, the remaining points define an epsilon-accurate Pareto set of the given design space.
We have derived theoretical bounds on the number of iterations required by the algorithm to generate a prediction with the level of accuracy (epsilon) and confidence (delta) specified by the user.e-PAL is an improved version of PAL[1]. Unlike PAL, e-PAL returns an epsilon-accurate Pareto front of the given design space. In addition, e-PAL reduces the number of computations required in each iteration of the algorithm, making it more suitable for large design spaces.
Benchmarks
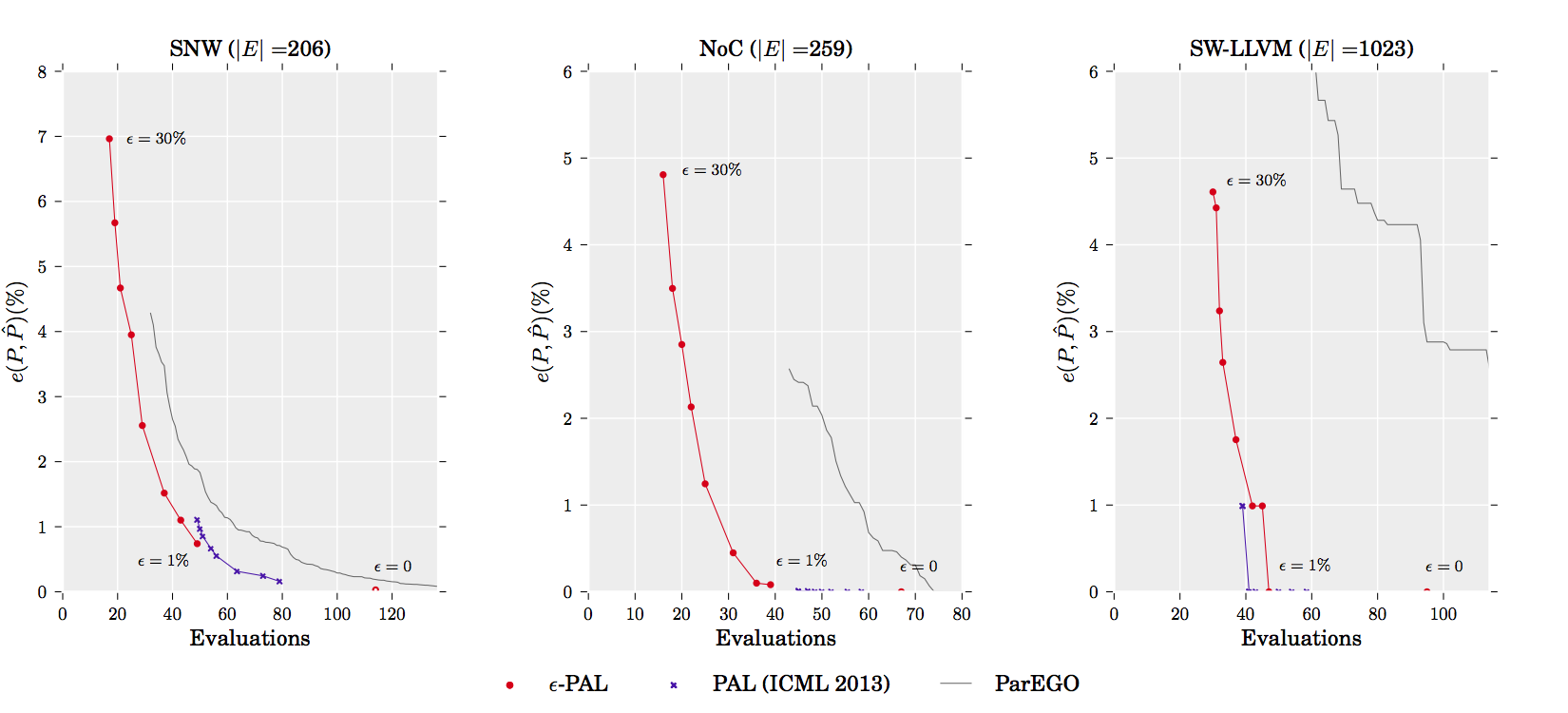
The plots below show the results of our experiments, performed based on data sets obtained in [3], [4] and [5].
In the y-axis, we show the accuracy of the Pareto front predicted when the algorithm has terminated. Accuracy is measured as the average maximum distance found between a point in the true pareto front and the closest point in the predicted Pareto front. The x-axis shows the number of designs that had to be evaluated in order to generate the prediction.
The results show that different accuracy/training-cost tradeoffs can be obtained by varying the value of epsilon. A larger epsilon causes e-PAL to stop earlier.
We compare the efficiency of e-PAL with those obtained with PAL and with the evolutionary algorithm ParEGO [6]. These results show that e-PAL in almost all cases significantly improves over PAL and ParEGO.
More details on these experiments can be found in [1].
Download
Our implementation of e-PAL can be downloaded here. This archive also contains the datasets used for our experiments presented in [1]. Detailed instructions on how to use this software are included in the README file.This implementation is written in Matlab, and uses the GPML libraries written by Carl Edward Rasmussen and Chris Williams [2]. e-PAL can be used for any number of objective functions, however this implementation is limited to two objective functions.
References
All our work on learning for optimization and autotuning.- Marcela Zuluaga, Andreas Krause and Markus Püschel
e-PAL: An Active Learning Approach to the Multi-Objective Optimization Problem
Journal of Machine Learning Research, Vol. 17, No. 104, pp. 1-32, 2016 - Marcela Zuluaga, Andreas Krause, Guillaume Sergent and Markus Püschel
Active Learning for Multi-Objective Optimization
Proc. International Conference on Machine Learning (ICML), 2013 - Marcela Zuluaga, Andreas Krause, Peter A. Milder and Markus Püschel
"Smart" Design Space Sampling to Predict Pareto-Optimal Solutions
Proc. Languages, Compilers, Tools and Theory for Embedded Systems (LCTES), pp. 119-128 , 2012 - Marcela Zuluaga, Peter A. Milder, and Markus Püschel
Computer Generation of Streaming Sorting Networks
Proc. Design Automation Conference (DAC), 2012 - Carl Edward Rasmussen and Christopher K. I. Williams
Gaussian Processes for Machine Learning
The MIT Press, 2006 - Oscar Almer, Nigel Topham, and Björn Franke
Learning-Based Approach to the Automated Design of MPSoC Networks
Proc. Architecture of Computing Systems (ARCS), 2011 - N. Siegmund, S. S. Kolesnikov, C. Kastner, S. Apel, D. Batoryx, M. Rosenmuller, and G. Saake
Predicting Performance via Automated Feature-Interaction Detection
Proc. Int'l Conference on Software Engineering (ICSE), 2012 - J. Knowles
ParEGO: a Hybrid Algorithm with Online Landscape Approximation for Expensive Multiobjective Optimization Problems
IEEE Trans. on Evolutionary Computation, 2006
Copyrights to many of the above papers are held by the publishers. The attached PDF files are preprints. It is understood that all persons copying this information will adhere to the terms and constraints invoked by each author's copyright. These works may not be reposted without the explicit permission of the copyright holder. Some links to papers above connect to IEEE Xplore with permission from IEEE, and viewers must follow all of IEEE's copyright policies.
