The Problem: Moore's Law and Fast Numerical Software
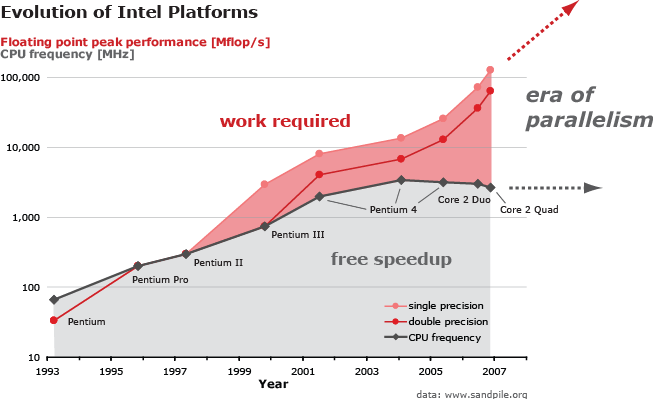
Computing platforms have hit the "power-wall:" CPU frequency scaling has come to an end (around 3 GHz); performance gains are achieved by increasing the platform's parallelism through multiple cores on a single die or SIMD vector instructions.This situation is shown in the figure. Frequency scaling means an automatic (free) speedup for numerical software (gray region); to achieve the maximal performance possible (light-red region) work is required. Namely, algorithm and implementation have to be carefully tuned to make optimal use of the platform's parallelism. The gap is increasing: implementing numerical software becomes more and more difficult.
 |
|
The evolution of computing platform's peak performance versus CPU frequency explains why high performance software development becomes increasingly harder
|
As a consequence, the performance gap between a "reasonable'' implementation and the best possible implementation is increasing. The next figure demonstrates this for the discrete Fourier transform (DFT). The plot shows the performance achieved by the implementation from Numerical Recipes (gray line) and the best achievable performance (red line) on a recent Intel Core platform. The difference is around 12x for small sizes and up to 25x for large sizes where multiple cores can be used.
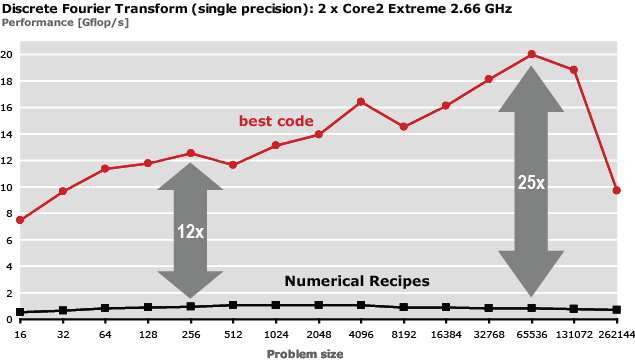 |
| The performance difference between a "reasonable implementation" and the best available code. The operations count is roughly the same. |
So what do we do about this? Current practice is to reimplement and reoptimize the same functionality (DFT, basic linear algebra subroutines = BLAS, and many other numerical kernels) whenever a new platform comes out. A better approach is to automate part of the implementation or optimization (often called Automatic Performance Tuning):
- recent Proc. IEEE special issue on this topic
- collection of links to projects in this new area
In Spiral, our attack of this problem is ambitious: we aim to "teach" computers to write fast libraries (software and hardware, i.e., Verilog) that are optimized for all available platform features. Everything is automated: push-button code generation. For linear transforms we have achieved this goal to some extent (see some benchmarks); other functionality is current research
How does one teach a computer to write libraries as fast as those carefully tuned by a human? The main challenge is to "conquer the high abstraction level for automation." This means the knowledge about available algorithms and about algorithm optimization has to be formalized into a form suitable for a computer. This way, difficult optimizations, such as parallelization, can be performed automatically at a high level of abstraction, and different algorithms can be generated and evaluated. This is schematically shown in the figure.
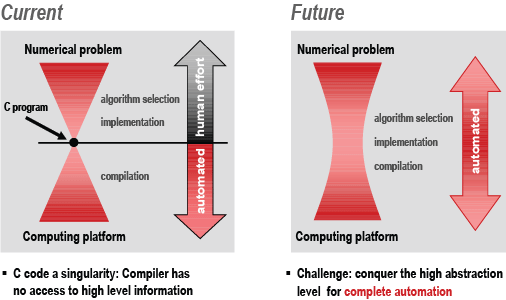 |
| Contrasting approaches to developing fast libraries |
Spiral is an example of this philosophy. See our latest papers:
