Multiplierless Constant Multiplication

We have developed algorithms and tools that generate multiplier blocks that multiply by one or several constants "multiplierless," that is, using only additions, subtractions, and shifts.

Overview

A multiplication by a fixed-point constant can be done "multiplierless" using additions (or subtractions) and shifts only. This is relevant for hardware implementation to avoid costly multipliers, but may also be beneficial for software implementations, for example, for embedded processors. As a simple example, y = 5x can be computed as

y = (x<<2) + x.

Such a solution is called a multiplier block.

For a given constant c, the problem is to find a multiplier block with the least number of adds/subtracts. This problem and two extensions are visualized on the right. We have developed algorithms and online generators for each of the problems.

Finding an optimal solution for the these problems is NP complete [1]. Thus our algorithms find only a close-to-optimal solution. Note that the three problems are related to, but fundamentally different from the adder chain problem discussed in detail in [2].

References

  1. Cappello, P. R. and Steiglitz, K.
    Some complexity issues in digital signal processing
    IEEE Transactions on Acoustics, Speech, and Signal Processing ASSP-32(5), pp. 1037-1041, 1984
  2. Knuth, D.
    The Art of Computer Programming: Seminumerical Algorithms, Vol. 2
    Addison-Wesley, 1969

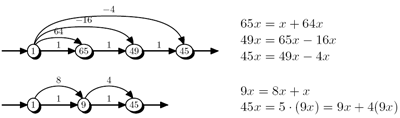
Single constant multiplication (SCM)

A straightforward way of multiplying by a given constant c using add/subtracts and shifts only can be read off from the bit representation of c. We call it the binary method. The well-known CSD (canonical signed digit) recoding reduces the number of add/subtracts required. The smallest example where CSD fails to produce the optimal solution is c=45 (CSD is above, the optimal below):

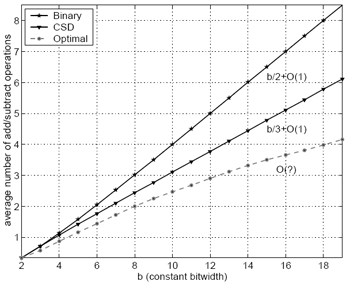
The optimal solution is only known for constants of bitwidth b<= 19 [1]. A comparison is shown in the figure.

For larger bitwidths our heuristic method (which works for any number of constants) produces good solutions [2].

Online generator for single (and multiple) constant multiplier blocks.

References

  1. Gustafsson, O., Dempster, A. G., and Wanhammar, L.
    Extended results for minimum-adder constant integer multipliers
    IEEE International Symposium on Circuits and Systems, 2002
  2. Yevgen Voronenko and Markus Püschel
    Multiplierless Multiple Constant Multiplication
    ACM Transactions on Algorithms, Vol. 3, No. 2, 2007

Copyrights to many of the above papers are held by the publishers. The attached PDF files are preprints. It is understood that all persons copying this information will adhere to the terms and constraints invoked by each author's copyright. These works may not be reposted without the explicit permission of the copyright holder. Some links to papers above connect to IEEE Xplore with permission from IEEE, and viewers must follow all of IEEE's copyright policies.

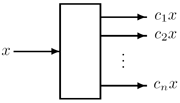
Multiplier Blocks

Single constant multiplication (SCM)

Given a constant c, find a multiplier block for the multiplication by c with the least number of add/subtracts.

Online generator or more information on the left.

Multiple constant multiplication (MCM) parallel

Given a set of n constants c1, ..., cn, find a multiplier block for the parallel multiplication with these constants with the least number of add/subtracts.

Online generator or more information.

Multiple constant multiplication (MCM) multiplexed

Given a set of n constants c1, ..., cn, find a multiplier block for the multiplexed multiplication based on a control input i. In this case, multiplexers are needed in the multiplier block. The objective we considered is area minimization for a hardware implementation.

Online generator or more information.